Page 42 - ตัวอย่าง หนังสือเรียน คณิต ม.2 เล่ม 2
P. 42
36
ความสัมพันธ์ระหว่างค่าเฉลี่ยเลขคณิต มัธยฐาน และฐานนิยม
ี
1. พ้นท่ของรูปส่เหลี่ยมผืนผ้าแต่ละรูปในฮิสโทแกรม จะมีค่าเท่ากับความถี่ของข้อมูลในแต่ละ
ื
ี
่
้
็
้
้
ั
ู
ั
่
่
็
่
ื
ี
ี
ี
้
ั
อันตรภาคชน ถ้าปรบรปหลายเหลียมใหเปนเส้นโค้งทเรยบและไม่เปนเหลียม พ้นทภายใตเสนโค้งทงหมด
้
จะแทนความถี่ของค่าจากการสังเกตท้งหมด ถ้าลักษณะเส้นโค้งท่ปรับไม่มีความเบ้ มีลักษณะเป็นรูป
ี
ั
ระฆังคว่า เราเรียกเส้นโค้งนี้ว่า เส้นโค้งปกติ และเรียกการแจกแจงของข้อมูลท่ทาให้เกิดเส้นโค้งปกติว่า
ี
ำ
ำ
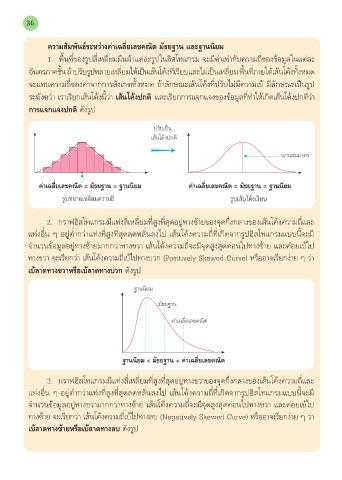
การแจกแจงปกติ ดังรูป
ปรับเป็น
เส้นโค้งปกติ
แกนสมมาตร
ค่าเฉลี่ยเลขคณิต = มัธยฐาน = ฐานนิยม ค่าเฉลี่ยเลขคณิต = มัธยฐาน = ฐานนิยม
รูปหลายเหลี่ยมความถี่ รูปเส้นโค้งเรียบ
2. กราฟฮิสโทแกรมมีแท่งส่เหลี่ยมท่สูงท่สุดอยู่ทางซ้ายของจุดกึ่งกลางของเส้นโค้งความถี่และ
ี
ี
ี
ี
ี
ื
แท่งอ่น ๆ อยู่ตำ่ากว่าแท่งท่สูงท่สุดลดหล่นลงไป เส้นโค้งความถี่ท่เกิดจากรูปฮิสโทแกรมแบบนี้จะมี
ี
ั
ำ
จานวนข้อมูลอยู่ทางซ้ายมากกว่าทางขวา เส้นโค้งความถี่จะมีจุดสูงสุดค่อนไปทางซ้าย และค่อยเบ้ไป
ทางขวา จะเรียกว่า เส้นโค้งความถี่เบ้ไปทางบวก (Positively Skewed Curve) หรืออาจเรียกง่าย ๆ ว่า
เบ้ลาดทางขวาหรือเบ้ลาดทางบวก ดังรูป
ฐานนิยม
มัธยฐาน
ค่าเฉลี่ยเลขคณิต
ฐานนิยม < มัธยฐาน < ค่าเฉลี่ยเลขคณิต
3. กราฟฮิสโทแกรมมีแท่งส่เหลี่ยมท่สูงท่สุดอยู่ทางขวาของจุดกึ่งกลางของเส้นโค้งความถี่และ
ี
ี
ี
แท่งอื่น ๆ อยู่ตำ่ากว่าแท่งท่สูงท่สุดลดหลั่นลงไป เส้นโค้งความถี่ท่เกิดจากรูปฮิสโทแกรมแบบนี้จะมี
ี
ี
ี
ำ
จานวนข้อมูลอยู่ทางขวามากกว่าทางซ้าย เส้นโค้งความถี่จะมีจุดสูงสุดค่อนไปทางขวา และค่อยเบ้ไป
ทางซ้าย จะเรียกว่า เส้นโค้งความถี่เบ้ไปทางลบ (Negatively Skewed Curve) หรืออาจเรียกง่าย ๆ ว่า
เบ้ลาดทางซ้ายหรือเบ้ลาดทางลบ ดังรูป